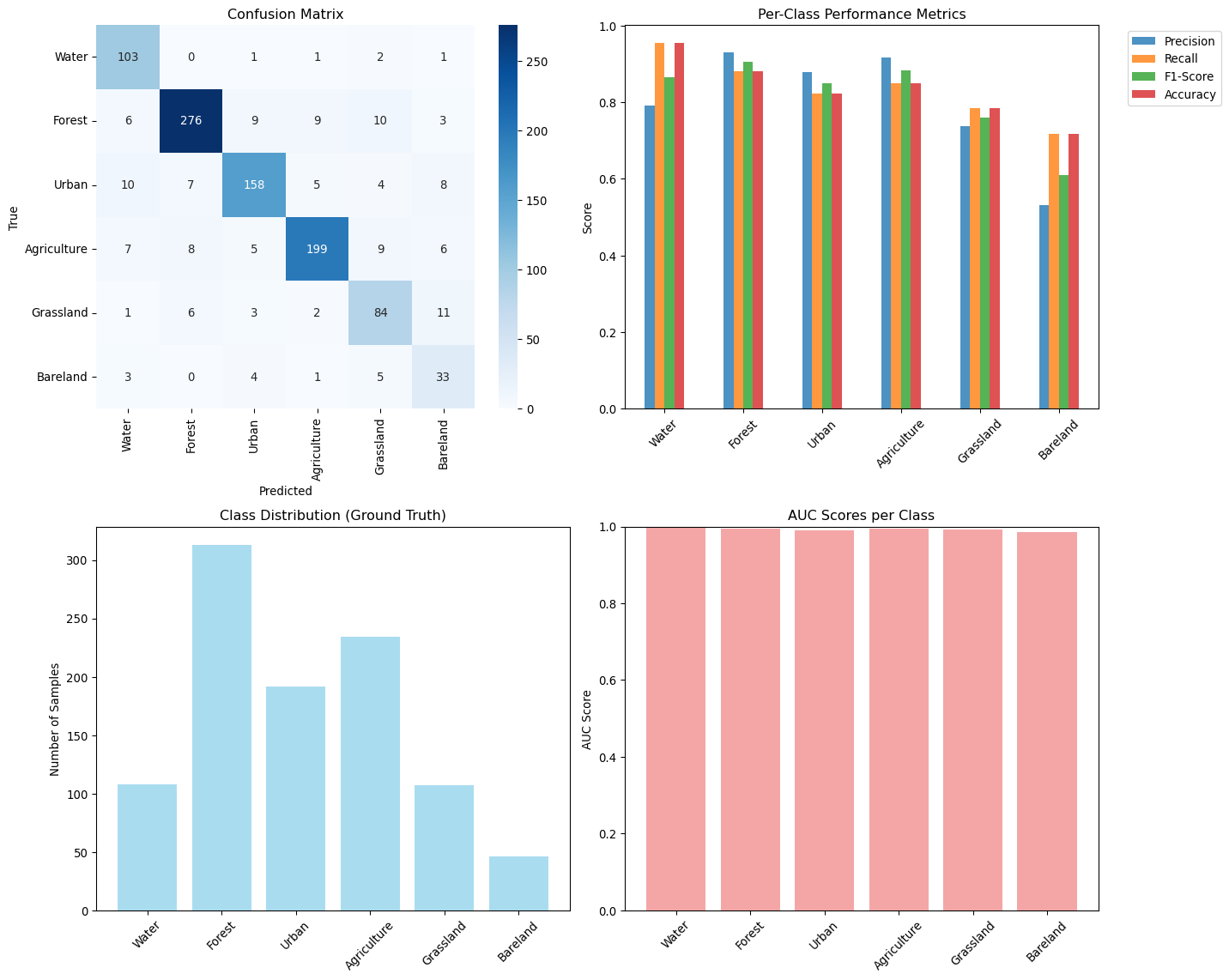
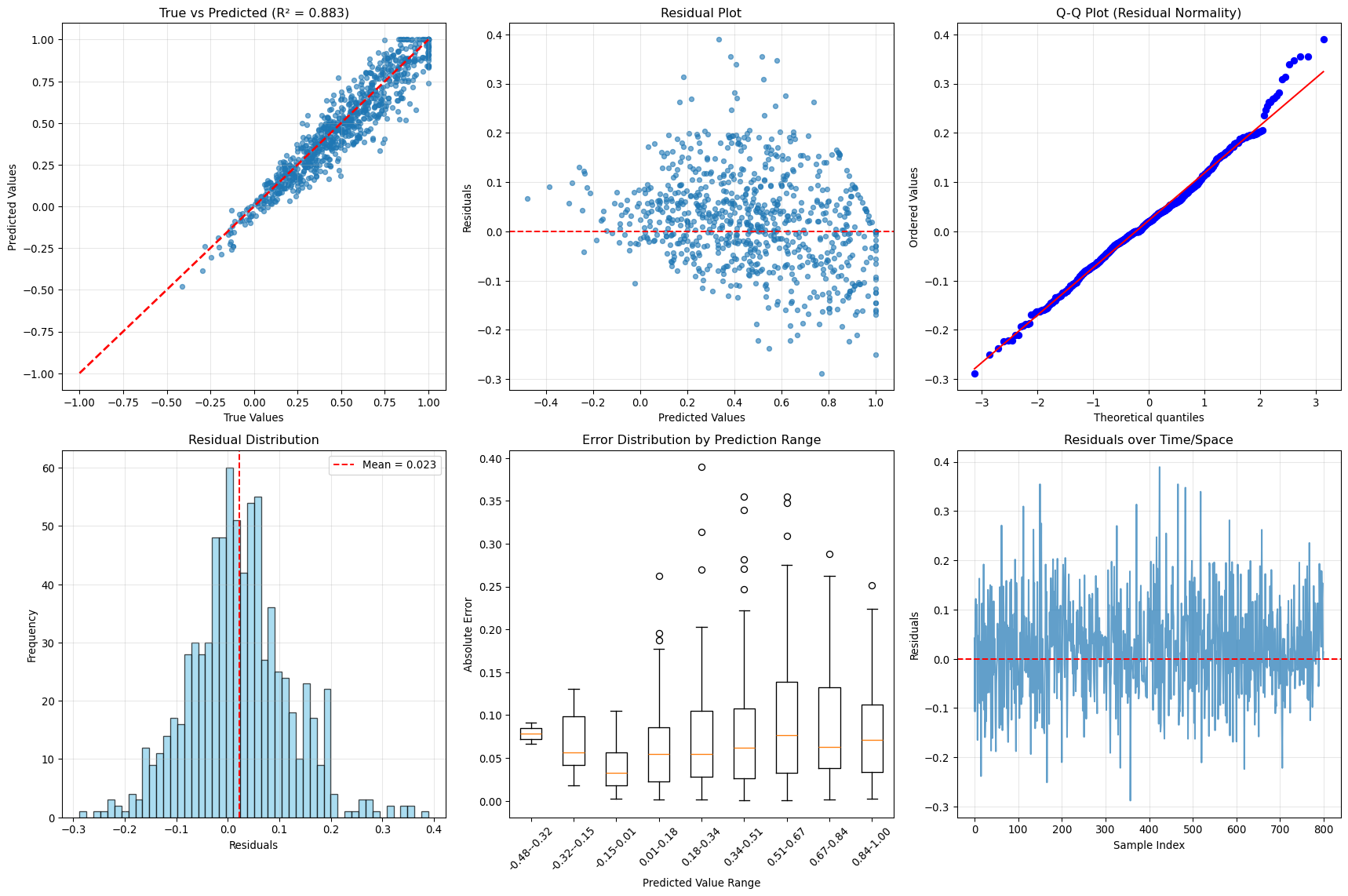
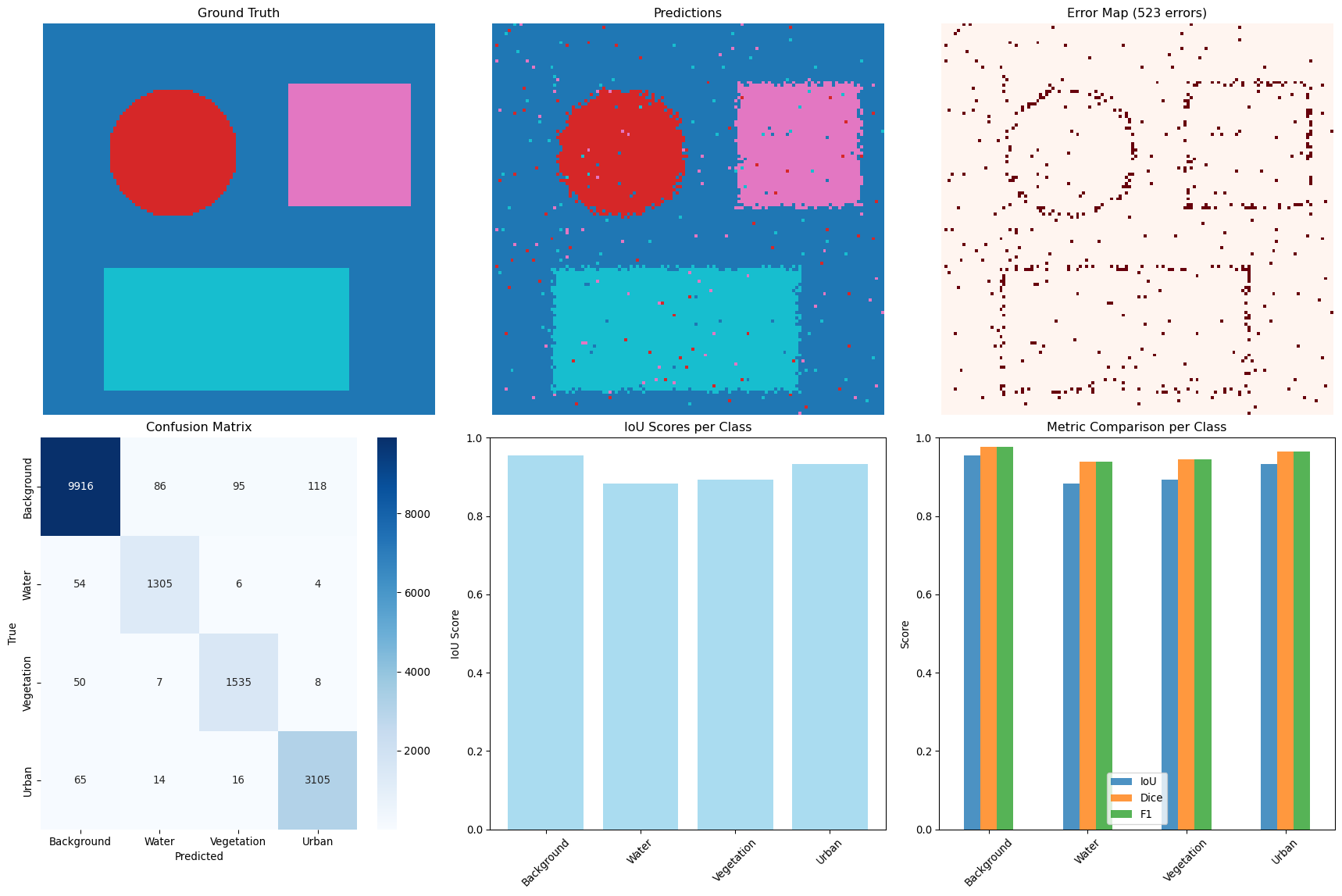
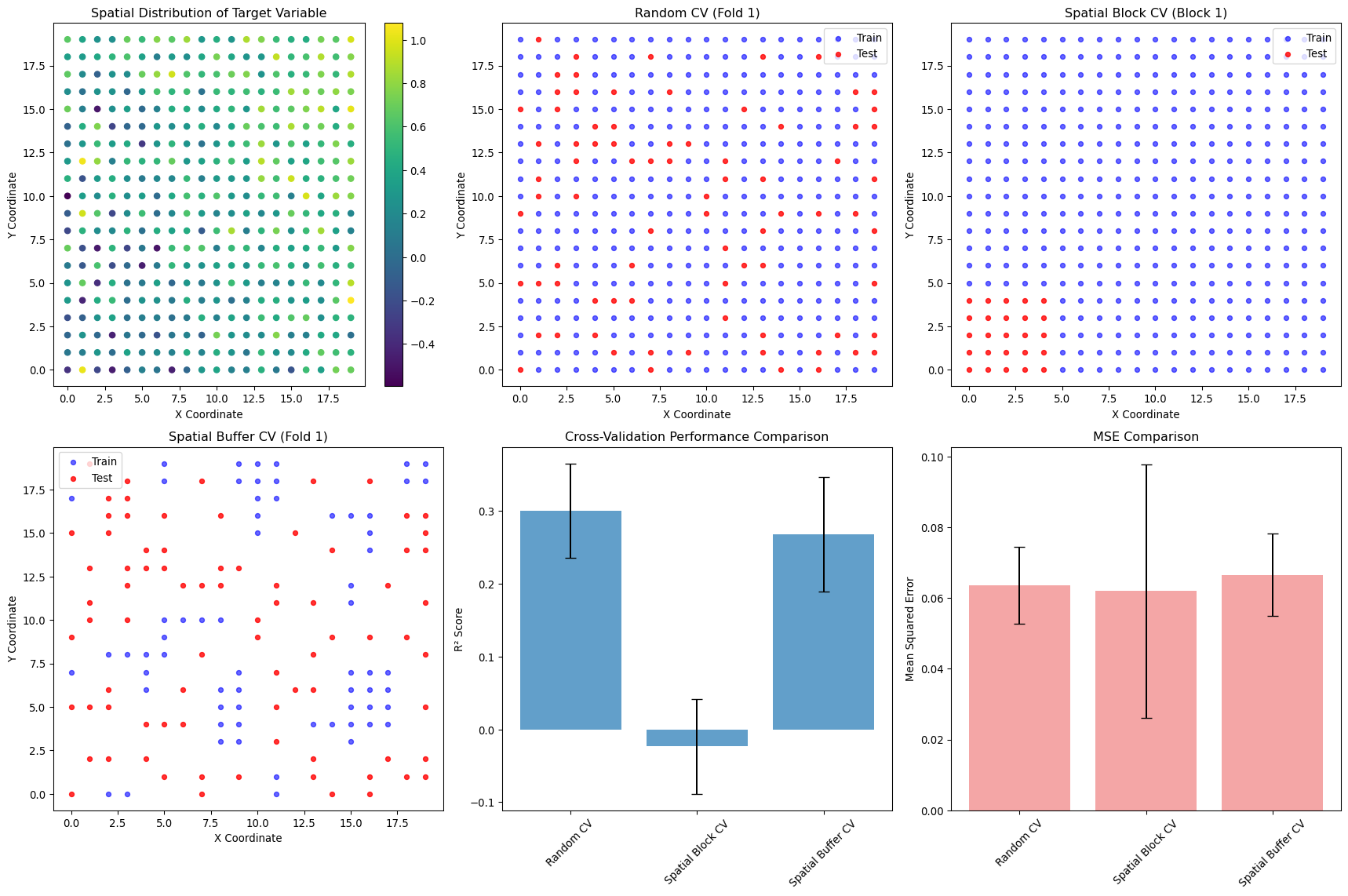
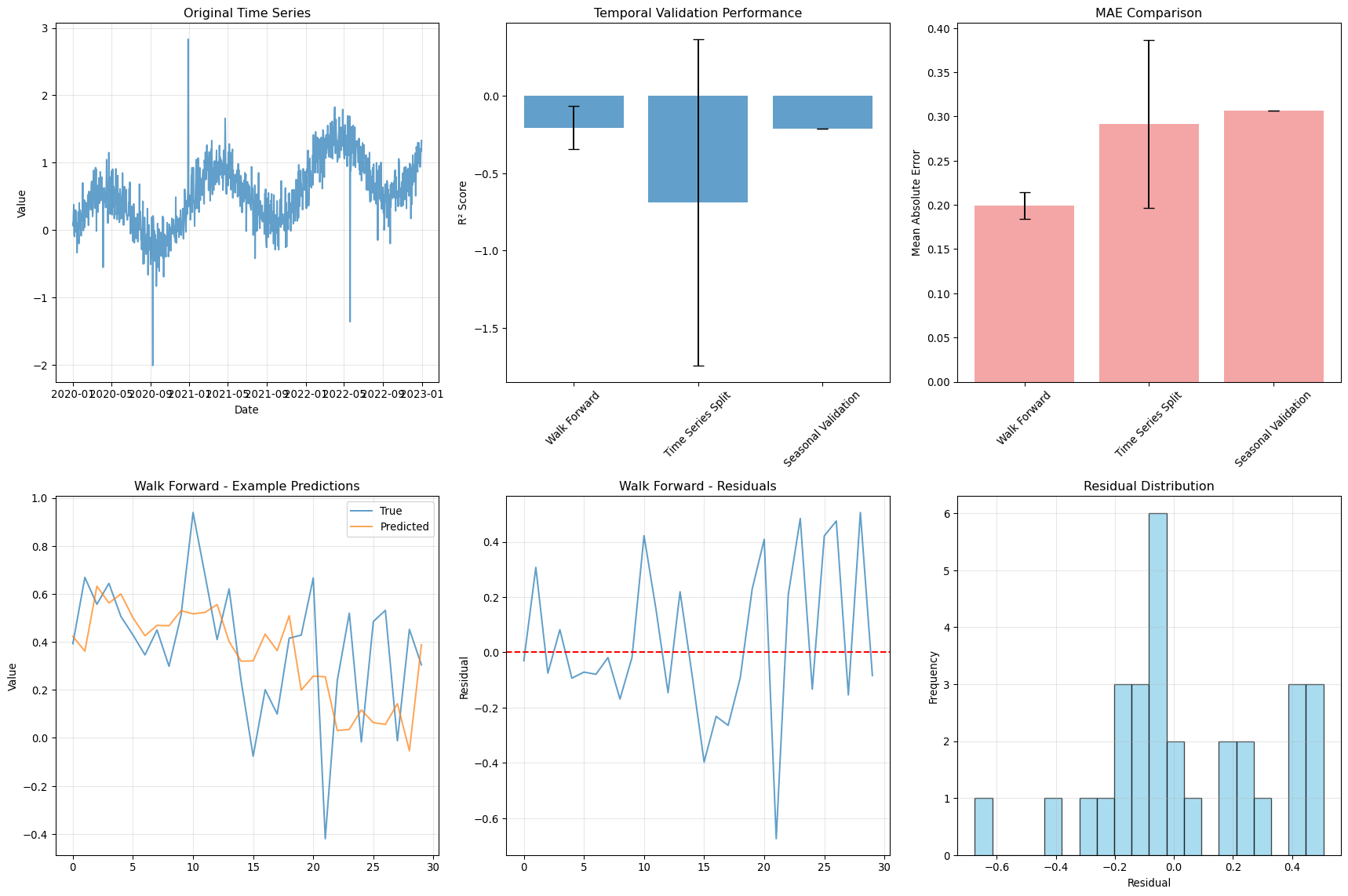
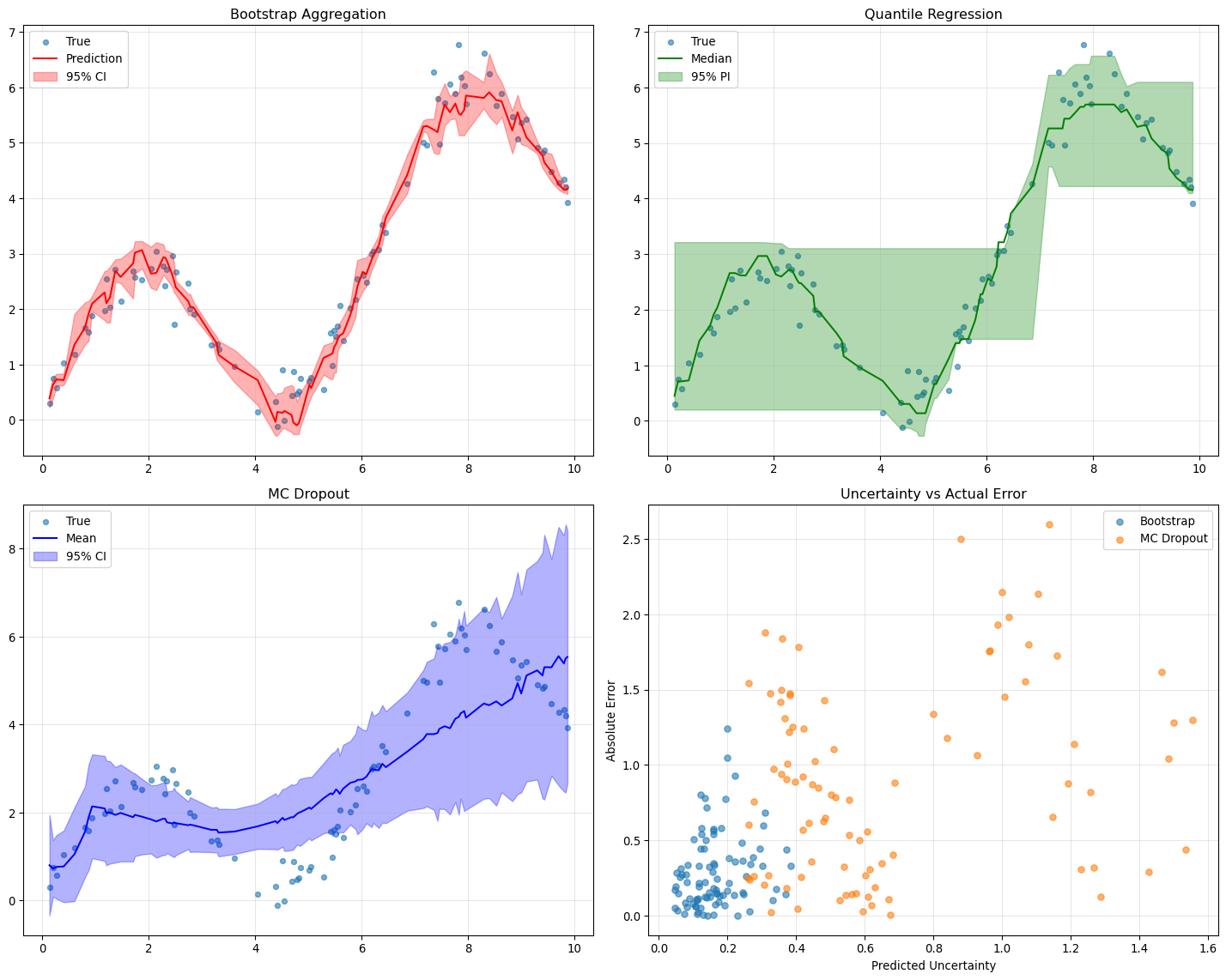
Model evaluation in geospatial AI requires specialized metrics and validation strategies that account for spatial dependencies, temporal variations, and domain-specific requirements. This cheatsheet covers comprehensive evaluation approaches.
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.metrics import accuracy_score, precision_recall_fscore_support, confusion_matrix
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import seaborn as sns
from scipy import stats
from sklearn.model_selection import train_test_split
print(f"PyTorch version: {torch.__version__}")PyTorch version: 2.7.1def comprehensive_classification_evaluation():
"""Demonstrate comprehensive classification evaluation metrics"""
# Simulate classification results for land cover classification
np.random.seed(42)
num_samples = 1000
num_classes = 6
class_names = ['Water', 'Forest', 'Urban', 'Agriculture', 'Grassland', 'Bareland']
# Generate realistic predictions (imbalanced classes)
class_probs = [0.1, 0.3, 0.2, 0.25, 0.1, 0.05] # Different class frequencies
y_true = np.random.choice(num_classes, size=num_samples, p=class_probs)
# Generate predictions with class-dependent accuracy
y_pred = y_true.copy()
class_accuracies = [0.95, 0.88, 0.82, 0.85, 0.78, 0.70] # Different per-class accuracies
for i in range(num_classes):
class_mask = y_true == i
num_class_samples = class_mask.sum()
num_errors = int(num_class_samples * (1 - class_accuracies[i]))
if num_errors > 0:
error_indices = np.random.choice(np.where(class_mask)[0], num_errors, replace=False)
# Create confusion: assign to other classes
other_classes = [j for j in range(num_classes) if j != i]
y_pred[error_indices] = np.random.choice(other_classes, num_errors)
# Generate prediction probabilities
y_probs = np.zeros((num_samples, num_classes))
for i in range(num_samples):
# Create realistic probability distributions
true_class = y_true[i]
pred_class = y_pred[i]
# Base probabilities
base_probs = np.random.dirichlet([0.5] * num_classes)
# Boost true class probability
base_probs[true_class] += 0.5
# If prediction is correct, boost predicted class
if true_class == pred_class:
base_probs[pred_class] += 0.3
# Normalize
y_probs[i] = base_probs / base_probs.sum()
# Calculate comprehensive metrics
from sklearn.metrics import (accuracy_score, precision_recall_fscore_support,
classification_report, confusion_matrix,
roc_auc_score, average_precision_score)
# Basic metrics
accuracy = accuracy_score(y_true, y_pred)
precision, recall, f1, support = precision_recall_fscore_support(y_true, y_pred, average=None)
macro_precision, macro_recall, macro_f1, _ = precision_recall_fscore_support(y_true, y_pred, average='macro')
weighted_precision, weighted_recall, weighted_f1, _ = precision_recall_fscore_support(y_true, y_pred, average='weighted')
# Confusion matrix
cm = confusion_matrix(y_true, y_pred)
# Per-class accuracy
per_class_accuracy = cm.diagonal() / cm.sum(axis=1)
# Multiclass AUC (one-vs-rest)
auc_scores = []
for i in range(num_classes):
y_true_binary = (y_true == i).astype(int)
auc = roc_auc_score(y_true_binary, y_probs[:, i])
auc_scores.append(auc)
print("Classification Evaluation Results:")
print("="*50)
print(f"Overall Accuracy: {accuracy:.3f}")
print(f"Macro F1-Score: {macro_f1:.3f}")
print(f"Weighted F1-Score: {weighted_f1:.3f}")
print("\nPer-Class Metrics:")
print("-" * 80)
print(f"{'Class':<12} {'Precision':<10} {'Recall':<10} {'F1-Score':<10} {'Accuracy':<10} {'AUC':<10} {'Support':<10}")
print("-" * 80)
for i, class_name in enumerate(class_names):
print(f"{class_name:<12} {precision[i]:<10.3f} {recall[i]:<10.3f} {f1[i]:<10.3f} {per_class_accuracy[i]:<10.3f} {auc_scores[i]:<10.3f} {support[i]:<10.0f}")
# Visualizations
fig, axes = plt.subplots(2, 2, figsize=(15, 12))
# Confusion Matrix
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues',
xticklabels=class_names, yticklabels=class_names, ax=axes[0,0])
axes[0,0].set_title('Confusion Matrix')
axes[0,0].set_xlabel('Predicted')
axes[0,0].set_ylabel('True')
# Per-class metrics
metrics_df = pd.DataFrame({
'Precision': precision,
'Recall': recall,
'F1-Score': f1,
'Accuracy': per_class_accuracy
}, index=class_names)
metrics_df.plot(kind='bar', ax=axes[0,1], alpha=0.8)
axes[0,1].set_title('Per-Class Performance Metrics')
axes[0,1].set_ylabel('Score')
axes[0,1].tick_params(axis='x', rotation=45)
axes[0,1].legend(bbox_to_anchor=(1.05, 1), loc='upper left')
# Class distribution
unique, counts = np.unique(y_true, return_counts=True)
axes[1,0].bar(class_names, counts, color='skyblue', alpha=0.7)
axes[1,0].set_title('Class Distribution (Ground Truth)')
axes[1,0].set_ylabel('Number of Samples')
axes[1,0].tick_params(axis='x', rotation=45)
# AUC scores
axes[1,1].bar(class_names, auc_scores, color='lightcoral', alpha=0.7)
axes[1,1].set_title('AUC Scores per Class')
axes[1,1].set_ylabel('AUC Score')
axes[1,1].tick_params(axis='x', rotation=45)
axes[1,1].set_ylim(0, 1)
plt.tight_layout()
plt.show()
return {
'accuracy': accuracy,
'precision': precision,
'recall': recall,
'f1': f1,
'confusion_matrix': cm,
'auc_scores': auc_scores,
'y_true': y_true,
'y_pred': y_pred,
'y_probs': y_probs
}
classification_results = comprehensive_classification_evaluation()Classification Evaluation Results:
==================================================
Overall Accuracy: 0.853
Macro F1-Score: 0.812
Weighted F1-Score: 0.856
Per-Class Metrics:
--------------------------------------------------------------------------------
Class Precision Recall F1-Score Accuracy AUC Support
--------------------------------------------------------------------------------
Water 0.792 0.954 0.866 0.954 0.996 108
Forest 0.929 0.882 0.905 0.882 0.994 313
Urban 0.878 0.823 0.849 0.823 0.990 192
Agriculture 0.917 0.850 0.882 0.850 0.994 234
Grassland 0.737 0.785 0.760 0.785 0.993 107
Bareland 0.532 0.717 0.611 0.717 0.985 46 
def comprehensive_regression_evaluation():
"""Demonstrate comprehensive regression evaluation metrics"""
# Simulate regression results for vegetation index prediction
np.random.seed(42)
num_samples = 800
# Generate realistic NDVI values (target)
# Simulate seasonal pattern with spatial variation
time_component = np.sin(np.linspace(0, 4*np.pi, num_samples)) * 0.3
spatial_component = np.random.normal(0, 0.2, num_samples)
noise = np.random.normal(0, 0.1, num_samples)
y_true = 0.5 + time_component + spatial_component + noise
y_true = np.clip(y_true, -1, 1) # NDVI range
# Generate predictions with realistic errors
# Add heteroscedastic noise (error depends on true value)
prediction_noise = np.random.normal(0, 0.05 + 0.1 * np.abs(y_true))
bias = -0.02 # Slight systematic bias
y_pred = y_true + prediction_noise + bias
y_pred = np.clip(y_pred, -1, 1)
# Calculate comprehensive regression metrics
mae = mean_absolute_error(y_true, y_pred)
mse = mean_squared_error(y_true, y_pred)
rmse = np.sqrt(mse)
r2 = r2_score(y_true, y_pred)
# Additional metrics
def mean_absolute_percentage_error(y_true, y_pred):
"""Calculate MAPE, handling near-zero values"""
mask = np.abs(y_true) > 1e-6
return np.mean(np.abs((y_true[mask] - y_pred[mask]) / y_true[mask])) * 100
def symmetric_mean_absolute_percentage_error(y_true, y_pred):
"""Calculate symmetric MAPE"""
return np.mean(2 * np.abs(y_true - y_pred) / (np.abs(y_true) + np.abs(y_pred))) * 100
mape = mean_absolute_percentage_error(y_true, y_pred)
smape = symmetric_mean_absolute_percentage_error(y_true, y_pred)
# Residual analysis
residuals = y_true - y_pred
# Statistical tests
# Shapiro-Wilk test for normality of residuals
shapiro_stat, shapiro_p = stats.shapiro(residuals[:100]) # Sample for computational efficiency
# Durbin-Watson test for autocorrelation (simplified)
def durbin_watson(residuals):
"""Calculate Durbin-Watson statistic"""
diff = np.diff(residuals)
return np.sum(diff**2) / np.sum(residuals**2)
dw_stat = durbin_watson(residuals)
# Quantile-based metrics
q25_error = np.percentile(np.abs(residuals), 25)
median_error = np.median(np.abs(residuals))
q75_error = np.percentile(np.abs(residuals), 75)
q95_error = np.percentile(np.abs(residuals), 95)
print("Regression Evaluation Results:")
print("="*50)
print(f"Mean Absolute Error (MAE): {mae:.4f}")
print(f"Mean Squared Error (MSE): {mse:.4f}")
print(f"Root Mean Squared Error (RMSE): {rmse:.4f}")
print(f"RΒ² Score: {r2:.4f}")
print(f"Mean Absolute Percentage Error (MAPE): {mape:.2f}%")
print(f"Symmetric MAPE: {smape:.2f}%")
print("\nResidual Analysis:")
print(f"Mean Residual (Bias): {residuals.mean():.4f}")
print(f"Std of Residuals: {residuals.std():.4f}")
print(f"Residual Skewness: {stats.skew(residuals):.4f}")
print(f"Residual Kurtosis: {stats.kurtosis(residuals):.4f}")
print(f"Shapiro-Wilk p-value: {shapiro_p:.4f}")
print(f"Durbin-Watson statistic: {dw_stat:.4f}")
print("\nQuantile-based Error Analysis:")
print(f"25th percentile error: {q25_error:.4f}")
print(f"Median error: {median_error:.4f}")
print(f"75th percentile error: {q75_error:.4f}")
print(f"95th percentile error: {q95_error:.4f}")
# Visualizations
fig, axes = plt.subplots(2, 3, figsize=(18, 12))
# Scatter plot: True vs Predicted
axes[0,0].scatter(y_true, y_pred, alpha=0.6, s=20)
axes[0,0].plot([-1, 1], [-1, 1], 'r--', lw=2) # Perfect prediction line
axes[0,0].set_xlabel('True Values')
axes[0,0].set_ylabel('Predicted Values')
axes[0,0].set_title(f'True vs Predicted (RΒ² = {r2:.3f})')
axes[0,0].grid(True, alpha=0.3)
# Residual plot
axes[0,1].scatter(y_pred, residuals, alpha=0.6, s=20)
axes[0,1].axhline(y=0, color='r', linestyle='--')
axes[0,1].set_xlabel('Predicted Values')
axes[0,1].set_ylabel('Residuals')
axes[0,1].set_title('Residual Plot')
axes[0,1].grid(True, alpha=0.3)
# Q-Q plot for residual normality
stats.probplot(residuals, dist="norm", plot=axes[0,2])
axes[0,2].set_title('Q-Q Plot (Residual Normality)')
axes[0,2].grid(True, alpha=0.3)
# Residual histogram
axes[1,0].hist(residuals, bins=50, alpha=0.7, color='skyblue', edgecolor='black')
axes[1,0].axvline(residuals.mean(), color='red', linestyle='--', label=f'Mean = {residuals.mean():.3f}')
axes[1,0].set_xlabel('Residuals')
axes[1,0].set_ylabel('Frequency')
axes[1,0].set_title('Residual Distribution')
axes[1,0].legend()
axes[1,0].grid(True, alpha=0.3)
# Error distribution by predicted value ranges
pred_ranges = np.linspace(y_pred.min(), y_pred.max(), 10)
range_errors = []
range_labels = []
for i in range(len(pred_ranges)-1):
mask = (y_pred >= pred_ranges[i]) & (y_pred < pred_ranges[i+1])
if mask.sum() > 0:
range_errors.append(np.abs(residuals[mask]))
range_labels.append(f'{pred_ranges[i]:.2f}-{pred_ranges[i+1]:.2f}')
axes[1,1].boxplot(range_errors, labels=range_labels)
axes[1,1].set_xlabel('Predicted Value Range')
axes[1,1].set_ylabel('Absolute Error')
axes[1,1].set_title('Error Distribution by Prediction Range')
axes[1,1].tick_params(axis='x', rotation=45)
# Time series of residuals (if applicable)
axes[1,2].plot(residuals, alpha=0.7)
axes[1,2].axhline(y=0, color='r', linestyle='--')
axes[1,2].set_xlabel('Sample Index')
axes[1,2].set_ylabel('Residuals')
axes[1,2].set_title('Residuals over Time/Space')
axes[1,2].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
return {
'mae': mae, 'mse': mse, 'rmse': rmse, 'r2': r2,
'mape': mape, 'smape': smape,
'residuals': residuals,
'y_true': y_true, 'y_pred': y_pred
}
regression_results = comprehensive_regression_evaluation()Regression Evaluation Results:
==================================================
Mean Absolute Error (MAE): 0.0757
Mean Squared Error (MSE): 0.0098
Root Mean Squared Error (RMSE): 0.0990
RΒ² Score: 0.8835
Mean Absolute Percentage Error (MAPE): 23.17%
Symmetric MAPE: 23.04%
Residual Analysis:
Mean Residual (Bias): 0.0226
Std of Residuals: 0.0964
Residual Skewness: 0.2393
Residual Kurtosis: 0.6648
Shapiro-Wilk p-value: 0.3088
Durbin-Watson statistic: 1.9282
Quantile-based Error Analysis:
25th percentile error: 0.0259
Median error: 0.0596
75th percentile error: 0.1100
95th percentile error: 0.1929/var/folders/bs/x9tn9jz91cv6hb3q6p4djbmw0000gn/T/ipykernel_53516/1856061205.py:133: MatplotlibDeprecationWarning:
The 'labels' parameter of boxplot() has been renamed 'tick_labels' since Matplotlib 3.9; support for the old name will be dropped in 3.11.
def comprehensive_segmentation_evaluation():
"""Demonstrate comprehensive segmentation evaluation metrics"""
# Simulate segmentation results
np.random.seed(42)
height, width = 128, 128
num_classes = 4
class_names = ['Background', 'Water', 'Vegetation', 'Urban']
# Generate realistic ground truth segmentation mask
y_true = np.zeros((height, width), dtype=int)
# Create regions for different classes
# Water body (circular)
center_x, center_y = width//3, height//3
y_indices, x_indices = np.ogrid[:height, :width]
water_mask = (x_indices - center_x)**2 + (y_indices - center_y)**2 < (width//6)**2
y_true[water_mask] = 1
# Vegetation (upper right)
y_true[20:60, 80:120] = 2
# Urban (lower region)
y_true[80:120, 20:100] = 3
# Generate predictions with realistic errors
y_pred = y_true.copy()
# Add boundary errors
from scipy import ndimage
edges = ndimage.binary_dilation(ndimage.laplace(y_true) != 0)
# Randomly flip some edge pixels
edge_indices = np.where(edges)
num_edge_errors = len(edge_indices[0]) // 4
error_indices = np.random.choice(len(edge_indices[0]), num_edge_errors, replace=False)
for idx in error_indices:
y, x = edge_indices[0][idx], edge_indices[1][idx]
# Assign to random neighboring class
neighbors = [y_true[max(0,y-1):min(height,y+2), max(0,x-1):min(width,x+2)]]
unique_neighbors = np.unique(neighbors)
other_classes = [c for c in unique_neighbors if c != y_true[y, x]]
if other_classes:
y_pred[y, x] = np.random.choice(other_classes)
# Add some random noise
num_random_errors = (height * width) // 50
error_y = np.random.randint(0, height, num_random_errors)
error_x = np.random.randint(0, width, num_random_errors)
for y, x in zip(error_y, error_x):
y_pred[y, x] = np.random.randint(0, num_classes)
# Calculate segmentation metrics
def calculate_segmentation_metrics(y_true, y_pred, num_classes):
"""Calculate comprehensive segmentation metrics"""
# Flatten arrays
y_true_flat = y_true.flatten()
y_pred_flat = y_pred.flatten()
# Basic accuracy
accuracy = accuracy_score(y_true_flat, y_pred_flat)
# Per-class metrics
precision, recall, f1, support = precision_recall_fscore_support(
y_true_flat, y_pred_flat, average=None, zero_division=0
)
# Confusion matrix
cm = confusion_matrix(y_true_flat, y_pred_flat)
# IoU (Intersection over Union) per class
iou_scores = []
dice_scores = []
for i in range(num_classes):
# True positives, false positives, false negatives
tp = cm[i, i]
fp = cm[:, i].sum() - tp
fn = cm[i, :].sum() - tp
# IoU
iou = tp / (tp + fp + fn) if (tp + fp + fn) > 0 else 0
iou_scores.append(iou)
# Dice coefficient
dice = 2 * tp / (2 * tp + fp + fn) if (2 * tp + fp + fn) > 0 else 0
dice_scores.append(dice)
# Mean IoU
mean_iou = np.mean(iou_scores)
# Pixel accuracy (same as overall accuracy)
pixel_accuracy = accuracy
# Mean accuracy (average of per-class accuracies)
class_accuracies = cm.diagonal() / cm.sum(axis=1)
mean_accuracy = np.mean(class_accuracies)
# Frequency weighted IoU
class_frequencies = cm.sum(axis=1) / cm.sum()
freq_weighted_iou = np.sum(class_frequencies * iou_scores)
return {
'pixel_accuracy': pixel_accuracy,
'mean_accuracy': mean_accuracy,
'mean_iou': mean_iou,
'freq_weighted_iou': freq_weighted_iou,
'iou_scores': iou_scores,
'dice_scores': dice_scores,
'precision': precision,
'recall': recall,
'f1': f1,
'confusion_matrix': cm
}
metrics = calculate_segmentation_metrics(y_true, y_pred, num_classes)
print("Segmentation Evaluation Results:")
print("="*50)
print(f"Pixel Accuracy: {metrics['pixel_accuracy']:.4f}")
print(f"Mean Accuracy: {metrics['mean_accuracy']:.4f}")
print(f"Mean IoU: {metrics['mean_iou']:.4f}")
print(f"Frequency Weighted IoU: {metrics['freq_weighted_iou']:.4f}")
print("\nPer-Class Metrics:")
print("-" * 70)
print(f"{'Class':<12} {'IoU':<8} {'Dice':<8} {'Precision':<10} {'Recall':<10} {'F1':<8}")
print("-" * 70)
for i, class_name in enumerate(class_names):
print(f"{class_name:<12} {metrics['iou_scores'][i]:<8.3f} {metrics['dice_scores'][i]:<8.3f} "
f"{metrics['precision'][i]:<10.3f} {metrics['recall'][i]:<10.3f} {metrics['f1'][i]:<8.3f}")
# Visualizations
fig, axes = plt.subplots(2, 3, figsize=(18, 12))
# Ground truth
im1 = axes[0,0].imshow(y_true, cmap='tab10', vmin=0, vmax=num_classes-1)
axes[0,0].set_title('Ground Truth')
axes[0,0].axis('off')
# Predictions
im2 = axes[0,1].imshow(y_pred, cmap='tab10', vmin=0, vmax=num_classes-1)
axes[0,1].set_title('Predictions')
axes[0,1].axis('off')
# Error map
error_map = (y_true != y_pred).astype(int)
axes[0,2].imshow(error_map, cmap='Reds')
axes[0,2].set_title(f'Error Map ({error_map.sum()} errors)')
axes[0,2].axis('off')
# Confusion matrix
sns.heatmap(metrics['confusion_matrix'], annot=True, fmt='d', cmap='Blues',
xticklabels=class_names, yticklabels=class_names, ax=axes[1,0])
axes[1,0].set_title('Confusion Matrix')
axes[1,0].set_xlabel('Predicted')
axes[1,0].set_ylabel('True')
# Per-class IoU
axes[1,1].bar(class_names, metrics['iou_scores'], color='skyblue', alpha=0.7)
axes[1,1].set_title('IoU Scores per Class')
axes[1,1].set_ylabel('IoU Score')
axes[1,1].tick_params(axis='x', rotation=45)
axes[1,1].set_ylim(0, 1)
# Metrics comparison
metrics_comparison = pd.DataFrame({
'IoU': metrics['iou_scores'],
'Dice': metrics['dice_scores'],
'F1': metrics['f1']
}, index=class_names)
metrics_comparison.plot(kind='bar', ax=axes[1,2], alpha=0.8)
axes[1,2].set_title('Metric Comparison per Class')
axes[1,2].set_ylabel('Score')
axes[1,2].tick_params(axis='x', rotation=45)
axes[1,2].legend()
axes[1,2].set_ylim(0, 1)
plt.tight_layout()
plt.show()
return metrics, y_true, y_pred
segmentation_metrics, gt_mask, pred_mask = comprehensive_segmentation_evaluation()Segmentation Evaluation Results:
==================================================
Pixel Accuracy: 0.9681
Mean Accuracy: 0.9634
Mean IoU: 0.9164
Frequency Weighted IoU: 0.9387
Per-Class Metrics:
----------------------------------------------------------------------
Class IoU Dice Precision Recall F1
----------------------------------------------------------------------
Background 0.955 0.977 0.983 0.971 0.977
Water 0.884 0.939 0.924 0.953 0.939
Vegetation 0.894 0.944 0.929 0.959 0.944
Urban 0.932 0.965 0.960 0.970 0.965 
def demonstrate_spatial_cross_validation():
"""Demonstrate spatial cross-validation strategies"""
# Simulate spatial data with coordinates
np.random.seed(42)
# Generate spatial grid
grid_size = 20
x_coords = np.repeat(np.arange(grid_size), grid_size)
y_coords = np.tile(np.arange(grid_size), grid_size)
n_samples = len(x_coords)
# Generate spatially correlated features and target
# Create spatial autocorrelation structure
def spatial_correlation(x1, y1, x2, y2, correlation_range=5):
"""Calculate spatial correlation based on distance"""
distance = np.sqrt((x1 - x2)**2 + (y1 - y2)**2)
return np.exp(-distance / correlation_range)
# Generate correlated target variable
y = np.zeros(n_samples)
base_trend = 0.5 * (x_coords / grid_size) + 0.3 * (y_coords / grid_size)
for i in range(n_samples):
# Add spatially correlated noise
spatial_component = 0
for j in range(min(50, n_samples)): # Limit for computational efficiency
if i != j:
weight = spatial_correlation(x_coords[i], y_coords[i], x_coords[j], y_coords[j])
spatial_component += weight * np.random.normal(0, 0.1)
y[i] = base_trend[i] + spatial_component + np.random.normal(0, 0.2)
# Generate features
X = np.column_stack([
x_coords / grid_size, # Normalized x coordinate
y_coords / grid_size, # Normalized y coordinate
np.random.normal(0, 1, n_samples), # Random feature 1
np.random.normal(0, 1, n_samples), # Random feature 2
])
# Different cross-validation strategies
def random_cv_split(X, y, n_folds=5):
"""Standard random cross-validation"""
from sklearn.model_selection import KFold
kfold = KFold(n_splits=n_folds, shuffle=True, random_state=42)
return list(kfold.split(X))
def spatial_block_cv_split(x_coords, y_coords, n_blocks=4):
"""Spatial block cross-validation"""
# Divide space into blocks
x_blocks = np.linspace(x_coords.min(), x_coords.max(), int(np.sqrt(n_blocks))+1)
y_blocks = np.linspace(y_coords.min(), y_coords.max(), int(np.sqrt(n_blocks))+1)
folds = []
for i in range(len(x_blocks)-1):
for j in range(len(y_blocks)-1):
# Test block
test_mask = ((x_coords >= x_blocks[i]) & (x_coords < x_blocks[i+1]) &
(y_coords >= y_blocks[j]) & (y_coords < y_blocks[j+1]))
# Training set is everything else
train_mask = ~test_mask
if test_mask.sum() > 0 and train_mask.sum() > 0:
train_indices = np.where(train_mask)[0]
test_indices = np.where(test_mask)[0]
folds.append((train_indices, test_indices))
return folds
def spatial_buffer_cv_split(x_coords, y_coords, n_folds=5, buffer_distance=2):
"""Spatial cross-validation with buffer zones"""
from sklearn.model_selection import KFold
# First, get random splits
kfold = KFold(n_splits=n_folds, shuffle=True, random_state=42)
random_splits = list(kfold.split(range(len(x_coords))))
buffered_splits = []
for train_idx, test_idx in random_splits:
# Remove training samples too close to test samples
filtered_train_idx = []
for train_i in train_idx:
min_dist_to_test = float('inf')
for test_i in test_idx:
dist = np.sqrt((x_coords[train_i] - x_coords[test_i])**2 +
(y_coords[train_i] - y_coords[test_i])**2)
min_dist_to_test = min(min_dist_to_test, dist)
if min_dist_to_test >= buffer_distance:
filtered_train_idx.append(train_i)
if len(filtered_train_idx) > 0:
buffered_splits.append((np.array(filtered_train_idx), test_idx))
return buffered_splits
# Evaluate different CV strategies
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
def evaluate_cv_strategy(X, y, cv_splits, strategy_name):
"""Evaluate a cross-validation strategy"""
r2_scores = []
mse_scores = []
for fold, (train_idx, test_idx) in enumerate(cv_splits):
# Train model
model = LinearRegression()
model.fit(X[train_idx], y[train_idx])
# Predict on test set
y_pred = model.predict(X[test_idx])
# Calculate metrics
r2 = r2_score(y[test_idx], y_pred)
mse = mean_squared_error(y[test_idx], y_pred)
r2_scores.append(r2)
mse_scores.append(mse)
return {
'strategy': strategy_name,
'r2_mean': np.mean(r2_scores),
'r2_std': np.std(r2_scores),
'mse_mean': np.mean(mse_scores),
'mse_std': np.std(mse_scores),
'n_folds': len(cv_splits)
}
# Apply different CV strategies
random_splits = random_cv_split(X, y, n_folds=5)
block_splits = spatial_block_cv_split(x_coords, y_coords, n_blocks=16)
buffer_splits = spatial_buffer_cv_split(x_coords, y_coords, n_folds=5, buffer_distance=2)
# Evaluate strategies
results = []
results.append(evaluate_cv_strategy(X, y, random_splits, 'Random CV'))
results.append(evaluate_cv_strategy(X, y, block_splits, 'Spatial Block CV'))
results.append(evaluate_cv_strategy(X, y, buffer_splits, 'Spatial Buffer CV'))
# Display results
print("Spatial Cross-Validation Comparison:")
print("="*60)
print(f"{'Strategy':<20} {'RΒ² Mean':<10} {'RΒ² Std':<10} {'MSE Mean':<10} {'MSE Std':<10} {'Folds':<6}")
print("-" * 60)
for result in results:
print(f"{result['strategy']:<20} {result['r2_mean']:<10.3f} {result['r2_std']:<10.3f} "
f"{result['mse_mean']:<10.3f} {result['mse_std']:<10.3f} {result['n_folds']:<6}")
# Visualizations
fig, axes = plt.subplots(2, 3, figsize=(18, 12))
# Data distribution
scatter = axes[0,0].scatter(x_coords, y_coords, c=y, cmap='viridis', s=30)
axes[0,0].set_title('Spatial Distribution of Target Variable')
axes[0,0].set_xlabel('X Coordinate')
axes[0,0].set_ylabel('Y Coordinate')
plt.colorbar(scatter, ax=axes[0,0])
# Random CV example (first fold)
train_idx, test_idx = random_splits[0]
axes[0,1].scatter(x_coords[train_idx], y_coords[train_idx], c='blue', s=20, alpha=0.6, label='Train')
axes[0,1].scatter(x_coords[test_idx], y_coords[test_idx], c='red', s=20, alpha=0.8, label='Test')
axes[0,1].set_title('Random CV (Fold 1)')
axes[0,1].set_xlabel('X Coordinate')
axes[0,1].set_ylabel('Y Coordinate')
axes[0,1].legend()
# Block CV example (first fold)
if block_splits:
train_idx, test_idx = block_splits[0]
axes[0,2].scatter(x_coords[train_idx], y_coords[train_idx], c='blue', s=20, alpha=0.6, label='Train')
axes[0,2].scatter(x_coords[test_idx], y_coords[test_idx], c='red', s=20, alpha=0.8, label='Test')
axes[0,2].set_title('Spatial Block CV (Block 1)')
axes[0,2].set_xlabel('X Coordinate')
axes[0,2].set_ylabel('Y Coordinate')
axes[0,2].legend()
# Buffer CV example (first fold)
if buffer_splits:
train_idx, test_idx = buffer_splits[0]
axes[1,0].scatter(x_coords[train_idx], y_coords[train_idx], c='blue', s=20, alpha=0.6, label='Train')
axes[1,0].scatter(x_coords[test_idx], y_coords[test_idx], c='red', s=20, alpha=0.8, label='Test')
axes[1,0].set_title('Spatial Buffer CV (Fold 1)')
axes[1,0].set_xlabel('X Coordinate')
axes[1,0].set_ylabel('Y Coordinate')
axes[1,0].legend()
# Performance comparison
strategies = [r['strategy'] for r in results]
r2_means = [r['r2_mean'] for r in results]
r2_stds = [r['r2_std'] for r in results]
bars = axes[1,1].bar(strategies, r2_means, yerr=r2_stds, capsize=5, alpha=0.7)
axes[1,1].set_title('Cross-Validation Performance Comparison')
axes[1,1].set_ylabel('RΒ² Score')
axes[1,1].tick_params(axis='x', rotation=45)
# MSE comparison
mse_means = [r['mse_mean'] for r in results]
mse_stds = [r['mse_std'] for r in results]
bars = axes[1,2].bar(strategies, mse_means, yerr=mse_stds, capsize=5, alpha=0.7, color='lightcoral')
axes[1,2].set_title('MSE Comparison')
axes[1,2].set_ylabel('Mean Squared Error')
axes[1,2].tick_params(axis='x', rotation=45)
plt.tight_layout()
plt.show()
return results, X, y, x_coords, y_coords
spatial_cv_results, spatial_X, spatial_y, spatial_x, spatial_y = demonstrate_spatial_cross_validation()Spatial Cross-Validation Comparison:
============================================================
Strategy RΒ² Mean RΒ² Std MSE Mean MSE Std Folds
------------------------------------------------------------
Random CV 0.301 0.065 0.064 0.011 5
Spatial Block CV -0.023 0.065 0.062 0.036 16
Spatial Buffer CV 0.268 0.079 0.067 0.012 5 
def demonstrate_temporal_validation():
"""Demonstrate temporal validation strategies for time series data"""
# Generate temporal dataset
np.random.seed(42)
# Create time series with trend, seasonality, and noise
n_timesteps = 365 * 3 # 3 years of daily data
time_index = pd.date_range('2020-01-01', periods=n_timesteps, freq='D')
# Generate synthetic time series
t = np.arange(n_timesteps)
# Trend component
trend = 0.001 * t
# Seasonal components
annual_cycle = 0.5 * np.sin(2 * np.pi * t / 365)
weekly_cycle = 0.1 * np.sin(2 * np.pi * t / 7)
# Random noise
noise = np.random.normal(0, 0.2, n_timesteps)
# Combine components
y = trend + annual_cycle + weekly_cycle + noise
# Add some extreme events
extreme_events = np.random.choice(n_timesteps, 10, replace=False)
y[extreme_events] += np.random.normal(0, 2, 10)
# Create features (lagged values, moving averages, etc.)
def create_temporal_features(y, lookback_window=30):
"""Create temporal features for time series prediction"""
features = []
targets = []
for i in range(lookback_window, len(y)):
# Lagged values
lag_features = y[i-lookback_window:i]
# Statistical features
stat_features = [
np.mean(lag_features),
np.std(lag_features),
np.min(lag_features),
np.max(lag_features),
lag_features[-1], # Most recent value
lag_features[-7] # Value from a week ago
]
# Time features
day_of_year = (i % 365) / 365
day_of_week = (i % 7) / 7
# Combine all features
all_features = list(lag_features) + stat_features + [day_of_year, day_of_week]
features.append(all_features)
targets.append(y[i])
return np.array(features), np.array(targets)
X, y_target = create_temporal_features(y, lookback_window=7)
# Temporal validation strategies
def walk_forward_validation(X, y, n_splits=5, test_size=30):
"""Walk-forward (expanding window) validation"""
n_samples = len(X)
min_train_size = n_samples // 2
splits = []
for i in range(n_splits):
# Expanding training set
train_end = min_train_size + i * test_size
test_start = train_end
test_end = min(test_start + test_size, n_samples)
if test_end > test_start:
train_idx = np.arange(0, train_end)
test_idx = np.arange(test_start, test_end)
splits.append((train_idx, test_idx))
return splits
def time_series_split_validation(X, y, n_splits=5):
"""Time series split validation (rolling window)"""
from sklearn.model_selection import TimeSeriesSplit
tss = TimeSeriesSplit(n_splits=n_splits)
return list(tss.split(X))
def seasonal_validation(X, y, season_length=365):
"""Seasonal validation - train on some seasons, test on others"""
n_samples = len(X)
n_seasons = n_samples // season_length
splits = []
for test_season in range(1, n_seasons): # Skip first season for training
# Training: all seasons except test season
train_idx = []
for season in range(n_seasons):
if season != test_season:
season_start = season * season_length
season_end = min((season + 1) * season_length, n_samples)
train_idx.extend(range(season_start, season_end))
# Test: specific season
test_start = test_season * season_length
test_end = min((test_season + 1) * season_length, n_samples)
test_idx = list(range(test_start, test_end))
if len(train_idx) > 0 and len(test_idx) > 0:
splits.append((np.array(train_idx), np.array(test_idx)))
return splits
# Evaluate different temporal validation strategies
from sklearn.ensemble import RandomForestRegressor
def evaluate_temporal_strategy(X, y, cv_splits, strategy_name):
"""Evaluate temporal validation strategy"""
r2_scores = []
mae_scores = []
predictions_all = []
for fold, (train_idx, test_idx) in enumerate(cv_splits):
# Train model
model = RandomForestRegressor(n_estimators=50, random_state=42)
model.fit(X[train_idx], y[train_idx])
# Predict
y_pred = model.predict(X[test_idx])
# Metrics
r2 = r2_score(y[test_idx], y_pred)
mae = mean_absolute_error(y[test_idx], y_pred)
r2_scores.append(r2)
mae_scores.append(mae)
predictions_all.append((test_idx, y[test_idx], y_pred))
return {
'strategy': strategy_name,
'r2_mean': np.mean(r2_scores),
'r2_std': np.std(r2_scores),
'mae_mean': np.mean(mae_scores),
'mae_std': np.std(mae_scores),
'predictions': predictions_all,
'n_folds': len(cv_splits)
}
# Apply different strategies
walk_forward_splits = walk_forward_validation(X, y_target, n_splits=5)
ts_splits = time_series_split_validation(X, y_target, n_splits=5)
seasonal_splits = seasonal_validation(X, y_target, season_length=365)
# Evaluate strategies
temporal_results = []
temporal_results.append(evaluate_temporal_strategy(X, y_target, walk_forward_splits, 'Walk Forward'))
temporal_results.append(evaluate_temporal_strategy(X, y_target, ts_splits, 'Time Series Split'))
temporal_results.append(evaluate_temporal_strategy(X, y_target, seasonal_splits, 'Seasonal Validation'))
# Display results
print("Temporal Validation Comparison:")
print("="*60)
print(f"{'Strategy':<20} {'RΒ² Mean':<10} {'RΒ² Std':<10} {'MAE Mean':<10} {'MAE Std':<10} {'Folds':<6}")
print("-" * 60)
for result in temporal_results:
print(f"{result['strategy']:<20} {result['r2_mean']:<10.3f} {result['r2_std']:<10.3f} "
f"{result['mae_mean']:<10.3f} {result['mae_std']:<10.3f} {result['n_folds']:<6}")
# Visualizations
fig, axes = plt.subplots(2, 3, figsize=(18, 12))
# Original time series
axes[0,0].plot(time_index[:len(y)], y, alpha=0.7)
axes[0,0].set_title('Original Time Series')
axes[0,0].set_xlabel('Date')
axes[0,0].set_ylabel('Value')
axes[0,0].grid(True, alpha=0.3)
# Performance comparison
strategies = [r['strategy'] for r in temporal_results]
r2_means = [r['r2_mean'] for r in temporal_results]
r2_stds = [r['r2_std'] for r in temporal_results]
bars = axes[0,1].bar(strategies, r2_means, yerr=r2_stds, capsize=5, alpha=0.7)
axes[0,1].set_title('Temporal Validation Performance')
axes[0,1].set_ylabel('RΒ² Score')
axes[0,1].tick_params(axis='x', rotation=45)
# MAE comparison
mae_means = [r['mae_mean'] for r in temporal_results]
mae_stds = [r['mae_std'] for r in temporal_results]
bars = axes[0,2].bar(strategies, mae_means, yerr=mae_stds, capsize=5, alpha=0.7, color='lightcoral')
axes[0,2].set_title('MAE Comparison')
axes[0,2].set_ylabel('Mean Absolute Error')
axes[0,2].tick_params(axis='x', rotation=45)
# Example predictions for first strategy only (to fit in 2x3 grid)
if temporal_results:
result = temporal_results[0] # Show only first strategy
test_idx, y_true_fold, y_pred_fold = result['predictions'][0]
axes[1,0].plot(y_true_fold, alpha=0.7, label='True')
axes[1,0].plot(y_pred_fold, alpha=0.7, label='Predicted')
axes[1,0].set_title(f'{result["strategy"]} - Example Predictions')
axes[1,0].set_ylabel('Value')
axes[1,0].legend()
axes[1,0].grid(True, alpha=0.3)
# Residuals for first strategy
residuals = y_true_fold - y_pred_fold
axes[1,1].plot(residuals, alpha=0.7)
axes[1,1].axhline(y=0, color='r', linestyle='--')
axes[1,1].set_title(f'{result["strategy"]} - Residuals')
axes[1,1].set_ylabel('Residual')
axes[1,1].grid(True, alpha=0.3)
# Residual histogram
axes[1,2].hist(residuals, bins=20, alpha=0.7, color='skyblue', edgecolor='black')
axes[1,2].set_title('Residual Distribution')
axes[1,2].set_xlabel('Residual')
axes[1,2].set_ylabel('Frequency')
axes[1,2].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
return temporal_results, X, y_target, time_index
temporal_results, temp_X, temp_y, temp_time = demonstrate_temporal_validation()Temporal Validation Comparison:
============================================================
Strategy RΒ² Mean RΒ² Std MAE Mean MAE Std Folds
------------------------------------------------------------
Walk Forward -0.204 0.138 0.199 0.015 5
Time Series Split -0.688 1.055 0.291 0.095 5
Seasonal Validation -0.213 0.000 0.306 0.000 1 
def demonstrate_uncertainty_quantification():
"""Demonstrate uncertainty quantification methods"""
# Generate dataset with varying noise levels
np.random.seed(42)
n_samples = 300
X = np.linspace(0, 10, n_samples).reshape(-1, 1)
# Create heteroscedastic data (varying uncertainty)
noise_levels = 0.1 + 0.3 * np.abs(np.sin(X.flatten()))
y = 2 * np.sin(X.flatten()) + 0.5 * X.flatten() + np.random.normal(0, noise_levels)
# Split data
train_idx = np.random.choice(n_samples, int(0.7 * n_samples), replace=False)
test_idx = np.setdiff1d(np.arange(n_samples), train_idx)
X_train, X_test = X[train_idx], X[test_idx]
y_train, y_test = y[train_idx], y[test_idx]
# Method 1: Bootstrap Aggregation
def bootstrap_uncertainty(X_train, y_train, X_test, n_bootstrap=100):
"""Estimate uncertainty using bootstrap aggregation"""
from sklearn.ensemble import RandomForestRegressor
predictions = []
for i in range(n_bootstrap):
# Bootstrap sample
n_train = len(X_train)
bootstrap_idx = np.random.choice(n_train, n_train, replace=True)
X_boot = X_train[bootstrap_idx]
y_boot = y_train[bootstrap_idx]
# Train model
model = RandomForestRegressor(n_estimators=20, random_state=i)
model.fit(X_boot, y_boot)
# Predict
pred = model.predict(X_test)
predictions.append(pred)
predictions = np.array(predictions)
# Calculate statistics
mean_pred = np.mean(predictions, axis=0)
std_pred = np.std(predictions, axis=0)
# Confidence intervals
ci_lower = np.percentile(predictions, 2.5, axis=0)
ci_upper = np.percentile(predictions, 97.5, axis=0)
return mean_pred, std_pred, ci_lower, ci_upper
# Method 2: Quantile Regression
def quantile_regression_uncertainty(X_train, y_train, X_test, quantiles=[0.025, 0.5, 0.975]):
"""Estimate uncertainty using quantile regression"""
from sklearn.ensemble import GradientBoostingRegressor
predictions = {}
for q in quantiles:
model = GradientBoostingRegressor(loss='quantile', alpha=q, random_state=42)
model.fit(X_train, y_train)
predictions[q] = model.predict(X_test)
return predictions
# Method 3: Monte Carlo Dropout (simplified)
class MCDropoutModel(nn.Module):
"""Simple neural network with Monte Carlo Dropout"""
def __init__(self, input_dim=1, hidden_dim=50, dropout_rate=0.5):
super().__init__()
self.layers = nn.Sequential(
nn.Linear(input_dim, hidden_dim),
nn.ReLU(),
nn.Dropout(dropout_rate),
nn.Linear(hidden_dim, hidden_dim),
nn.ReLU(),
nn.Dropout(dropout_rate),
nn.Linear(hidden_dim, 1)
)
self.dropout_rate = dropout_rate
def forward(self, x):
return self.layers(x)
def predict_with_uncertainty(self, x, n_samples=100):
"""Predict with MC Dropout uncertainty"""
self.train() # Keep in training mode for dropout
predictions = []
with torch.no_grad():
for _ in range(n_samples):
pred = self(x)
predictions.append(pred.numpy())
predictions = np.array(predictions).squeeze()
if predictions.ndim == 1: # Single prediction
return predictions.mean(), predictions.std()
else: # Multiple predictions
return predictions.mean(axis=0), predictions.std(axis=0)
def mc_dropout_uncertainty(X_train, y_train, X_test):
"""Train MC Dropout model and get uncertainty estimates"""
# Convert to tensors
X_train_tensor = torch.FloatTensor(X_train)
y_train_tensor = torch.FloatTensor(y_train).unsqueeze(1)
X_test_tensor = torch.FloatTensor(X_test)
# Train model
model = MCDropoutModel()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
criterion = nn.MSELoss()
# Simple training loop
for epoch in range(200):
optimizer.zero_grad()
outputs = model(X_train_tensor)
loss = criterion(outputs, y_train_tensor)
loss.backward()
optimizer.step()
# Get predictions with uncertainty
mean_pred, std_pred = model.predict_with_uncertainty(X_test_tensor)
return mean_pred, std_pred
# Apply different uncertainty methods
print("Uncertainty Quantification Methods:")
print("="*50)
# Bootstrap
print("Running Bootstrap Aggregation...")
boot_mean, boot_std, boot_lower, boot_upper = bootstrap_uncertainty(X_train, y_train, X_test)
# Quantile regression
print("Running Quantile Regression...")
quantile_preds = quantile_regression_uncertainty(X_train, y_train, X_test)
# MC Dropout
print("Running MC Dropout...")
mc_mean, mc_std = mc_dropout_uncertainty(X_train, y_train, X_test)
# Calculate uncertainty metrics
def evaluate_uncertainty(y_true, mean_pred, std_pred=None, ci_lower=None, ci_upper=None):
"""Evaluate uncertainty estimation quality"""
# Prediction accuracy
mae = mean_absolute_error(y_true, mean_pred)
rmse = np.sqrt(mean_squared_error(y_true, mean_pred))
r2 = r2_score(y_true, mean_pred)
metrics = {'mae': mae, 'rmse': rmse, 'r2': r2}
if std_pred is not None:
# Uncertainty calibration
residuals = np.abs(y_true - mean_pred)
# Correlation between predicted uncertainty and actual errors
uncertainty_correlation = np.corrcoef(std_pred, residuals)[0, 1]
metrics['uncertainty_correlation'] = uncertainty_correlation
if ci_lower is not None and ci_upper is not None:
# Coverage probability (should be ~95% for 95% CI)
in_interval = (y_true >= ci_lower) & (y_true <= ci_upper)
coverage = np.mean(in_interval)
metrics['coverage'] = coverage
# Interval width
interval_width = np.mean(ci_upper - ci_lower)
metrics['mean_interval_width'] = interval_width
return metrics
# Evaluate methods
boot_metrics = evaluate_uncertainty(y_test, boot_mean, boot_std, boot_lower, boot_upper)
quantile_metrics = evaluate_uncertainty(y_test, quantile_preds[0.5],
ci_lower=quantile_preds[0.025],
ci_upper=quantile_preds[0.975])
mc_metrics = evaluate_uncertainty(y_test, mc_mean, mc_std)
print("\nUncertainty Evaluation Results:")
print("-" * 60)
print(f"{'Method':<20} {'MAE':<8} {'RMSE':<8} {'RΒ²':<8} {'Coverage':<10} {'Uncert.Corr':<12}")
print("-" * 60)
methods_data = [
('Bootstrap', boot_metrics),
('Quantile Reg.', quantile_metrics),
('MC Dropout', mc_metrics)
]
for method_name, metrics in methods_data:
coverage = metrics.get('coverage', 0)
uncert_corr = metrics.get('uncertainty_correlation', 0)
print(f"{method_name:<20} {metrics['mae']:<8.3f} {metrics['rmse']:<8.3f} {metrics['r2']:<8.3f} "
f"{coverage:<10.3f} {uncert_corr:<12.3f}")
# Visualizations
fig, axes = plt.subplots(2, 2, figsize=(15, 12))
# Sort test data for plotting
sort_idx = np.argsort(X_test.flatten())
X_test_sorted = X_test[sort_idx]
y_test_sorted = y_test[sort_idx]
# Bootstrap results
axes[0,0].scatter(X_test, y_test, alpha=0.6, s=20, label='True')
axes[0,0].plot(X_test_sorted, boot_mean[sort_idx], 'r-', label='Prediction')
axes[0,0].fill_between(X_test_sorted.flatten(),
boot_lower[sort_idx], boot_upper[sort_idx],
alpha=0.3, color='red', label='95% CI')
axes[0,0].set_title('Bootstrap Aggregation')
axes[0,0].legend()
axes[0,0].grid(True, alpha=0.3)
# Quantile regression
axes[0,1].scatter(X_test, y_test, alpha=0.6, s=20, label='True')
axes[0,1].plot(X_test_sorted, quantile_preds[0.5][sort_idx], 'g-', label='Median')
axes[0,1].fill_between(X_test_sorted.flatten(),
quantile_preds[0.025][sort_idx], quantile_preds[0.975][sort_idx],
alpha=0.3, color='green', label='95% PI')
axes[0,1].set_title('Quantile Regression')
axes[0,1].legend()
axes[0,1].grid(True, alpha=0.3)
# MC Dropout
axes[1,0].scatter(X_test, y_test, alpha=0.6, s=20, label='True')
axes[1,0].plot(X_test_sorted, mc_mean[sort_idx], 'b-', label='Mean')
# Calculate confidence intervals for MC Dropout
mc_lower = mc_mean - 1.96 * mc_std
mc_upper = mc_mean + 1.96 * mc_std
axes[1,0].fill_between(X_test_sorted.flatten(),
mc_lower[sort_idx], mc_upper[sort_idx],
alpha=0.3, color='blue', label='95% CI')
axes[1,0].set_title('MC Dropout')
axes[1,0].legend()
axes[1,0].grid(True, alpha=0.3)
# Uncertainty comparison
residuals_boot = np.abs(y_test - boot_mean)
residuals_mc = np.abs(y_test - mc_mean)
axes[1,1].scatter(boot_std, residuals_boot, alpha=0.6, label='Bootstrap', s=30)
axes[1,1].scatter(mc_std, residuals_mc, alpha=0.6, label='MC Dropout', s=30)
axes[1,1].set_xlabel('Predicted Uncertainty')
axes[1,1].set_ylabel('Absolute Error')
axes[1,1].set_title('Uncertainty vs Actual Error')
axes[1,1].legend()
axes[1,1].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
return methods_data
uncertainty_methods = demonstrate_uncertainty_quantification()Uncertainty Quantification Methods:
==================================================
Running Bootstrap Aggregation...
Running Quantile Regression...
Running MC Dropout...
Uncertainty Evaluation Results:
------------------------------------------------------------
Method MAE RMSE RΒ² Coverage Uncert.Corr
------------------------------------------------------------
Bootstrap 0.289 0.380 0.960 0.633 0.207
Quantile Reg. 0.279 0.366 0.963 0.900 0.000
MC Dropout 0.899 1.103 0.667 0.000 0.233 
Key concepts for model evaluation and validation: - Classification Metrics: Accuracy, precision, recall, F1, AUC, confusion matrices - Regression Metrics: MAE, MSE, RMSE, RΒ², residual analysis - Segmentation Metrics: IoU, Dice coefficient, pixel accuracy, mean accuracy - Spatial Validation: Block CV, buffer zones, spatial independence - Temporal Validation: Walk-forward, time series splits, seasonal validation - Uncertainty Quantification: Bootstrap, quantile regression, Monte Carlo dropout - Domain-Specific Considerations: Spatial autocorrelation, temporal dependencies - Comprehensive Evaluation: Multiple metrics, visualization, statistical testing